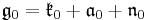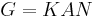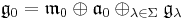Iwasawa decomposition

In mathematics, the Iwasawa decomposition KAN of a semisimple Lie group generalises the way a square real matrix can be written as a product of an orthogonal matrix and an upper triangular matrix (a consequence of Gram-Schmidt orthogonalization). It is named after Kenkichi Iwasawa, the Japanese mathematician who developed this method.

1 Definition
2 Examples
3 See also
4 References

Definition

G is a connected semisimple real Lie group.
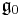$\mathfrak{g}_0$ is the Lie algebra of G
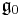$\mathfrak{g}$ is the complexification of $\mathfrak{g}_0$ .
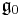
θ is a Cartan involution of $\mathfrak{g}_0$
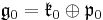$\mathfrak{g}_0 = \mathfrak{k}_0 \oplus \mathfrak{p}_0$ is the corresponding Cartan decomposition
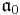$\mathfrak{a}_0$ is a maximal abelian subalgebra of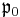 $\mathfrak{p}_0$
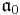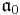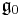Σ is the set of restricted roots of $\mathfrak{a}_0$ , corresponding to eigenvalues of $\mathfrak{a}_0$ acting on $\mathfrak{g}_0$ .
Σ⁺ is a choice of positive roots of Σ
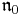$\mathfrak{n}_0$ is a nilpotent Lie algebra given as the sum of the root spaces of Σ⁺
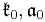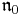K, A, N, are the Lie subgroups of G generated by $\mathfrak{k}_0, \mathfrak{a}_0$ and $\mathfrak{n}_0$ .

Then the Iwasawa decomposition of 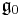$\mathfrak{g}_0$ is

$\mathfrak{g}_0 = \mathfrak{k}_0 %2B \mathfrak{a}_0 %2B \mathfrak{n}_0$

and the Iwasawa decomposition of G is

$G=KAN$

The dimension of A (or equivalently of 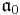$\mathfrak{a}_0$ ) is called the real rank of G.

Iwasawa decompositions also hold for some disconnected semisimple groups G, where K becomes a (disconnected) maximal compact subgroup provided the center of G is finite.

The restricted root space decomposition is

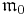$\mathfrak{g}_0 = \mathfrak{m}_0\oplus\mathfrak{a}_0\oplus_{\lambda\in\Sigma}\mathfrak{g}_{\lambda}$

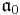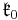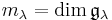where $\mathfrak{m}_0$ is the centralizer of $\mathfrak{a}_0$ in $\mathfrak{k}_0$ and $\mathfrak{g}_{\lambda} = \{X\in\mathfrak{g}_0: [H,X]=\lambda(H)X\;\;\forall H\in\mathfrak{a}_0 \}$ is the root space. The number $m_{\lambda}= \text{dim}\,\mathfrak{g}_{\lambda}$ is called the multiplicity of $\lambda$ .

Examples

If G=GL_n(R), then we can take K to be the orthogonal matrices, A to be the positive diagonal matrices, and N to be the unipotent group consisting of upper triangular matrices with 1s on the diagonal.

References

Fedenko, A.S.; Shtern, A.I. (2001), "Iwasawa decomposition", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=I/i053060
A. W. Knapp, Structure theory of semisimple Lie groups, in ISBN 0-8218-0609-2: Representation Theory and Automorphic Forms: Instructional Conference, International Centre for Mathematical Sciences, March 1996, Edinburgh, Scotland (Proceedings of Symposia in Pure Mathematics) by T. N. Bailey (Editor), Anthony W. Knapp (Editor)

Iwasawa, Kenkichi: On some types of topological groups. Annals of Mathematics (2) 50, (1949), 507–558.

Iwasawa decomposition

Contents

Definition

Examples

See also

References